[논문 리뷰] Towards Total Recall in Industrial Anomaly Detection

Introduction 

최근에 이상탐지 흐름 중 하나는 ImageNet classification 모델을 튜닝없이 사용하여 target distribution에 대한 common deep representation을 학습하는 것이다. fine grained defect segmentation은 high resolution feature를 사용하고 반면에 full image-level anomaly detection(structural deviation)은 higher abstraction level을 주로 사용한다. 이 방법의 단점은 Imagenet으로 학습된 모델의 higher level feature는 inudstrial environment에서 요구하는 abstrac feature와 유사하지 않다는 것이다. 

 

본 논문에서는 3가지 제안점을 두었다. 

1) maximizing nominal information available at test time 

2) reducing biases towards ImageNet classes

3) retaining high inference speeds 

 

또한 patch core는 mid-level network의 patch feature를 사용하기 때문에 ImageNet class에 대한 bias가 적고 이웃한 것들의 feature를 합산하기 떄문에 충분한 공간적 정보도 유지한다. 

 

Related work

Patch core는 SPADE와 PaDiM을 기반으로 한다. 

SPADE는 pretrained network에서 추출된 nominal feature에 memoryh-bank를 사용한다. Patch core는 이와 유사하게 memory bank(greedy coreset sampling) 및 nominal context를 더 활용하기 위해 neighbourhood aware patch-level feature를 사용한다. 

Patchcore는 PaDiM의 higher anomaly detection sensitivity(?)의 목적을 달성하는 것과 관련이 있다. Patch core는 patch memory bank를 사용하여 test 시에 모든 patch에 접근한다. (PaDiM은 each patch로 제한을 한다). 이렇게 함으로써 Patch core는 image alignment(정렬)에 덜 의존하고 larger nominal context를 고려할 수 있다. 

마지막으로 Patch core는 locally aware patch-feature score를 사용하여 local spatial variance를 인지하고 ImageNet class에 대한 bias을 줄일 수 있다. 

 

coreset selection 설명: https://kmhana.tistory.com/6

Active Learning을 위한 딥러닝 - Core-set

 

Method 

Locally aware patch features 

Patchcore는 ImageNet에 pretrained된 network를 사용한다. 

$ \phi_{i,j}$ = $ \phi_{j}(x_{i}) $가 뜻하는 것은 image $ x_{i} $의 hierarchy level j의 feature를 뜻한다. 

 

Network의 마지막 layer를 사용하면 2가지 문제점이 발생한다. 

1) localized nominal information을 잃어버린다 

2) ImageNet으로 훈련된 very deep and abstract features는 natural image classification을 분류하는데에 집중한다. 

 

여기서는 이를 해결하기 위해 mid-level features patch로 이루어진 memory bank $M$을 사용한다. 

 

Feature map $ \phi_{i,j} \subset \mathbb{R}^{c^{*} \times h^{*} \times w^{*}}$ 라고 한다면 $\phi_{i,j}(h,w) = \phi_{j}(x_{i}, h, w) \subset \mathbb{R}^{c^*}$ 특정 (h,w) 위치에서의 $c^*$ dimensional feature를 의미한다. 이상적으로는 each patch-representation이 충분한 receptive field size를 가져서 local spatial variation에 강건한 유의미한 비이상적인 context를 설명해야 한다 (단순히 local spatial variation을 보고 비정상을 판단하는게 아니라는 뜻인듯). 이는 network의 abstract feature를 사용하므로써 해결할 수 있지만 계속 말했듯이 ImageNet-specific 해진다. 

small spatial deviation에 강건하고 recpetive field size를 키우기 위해서 각 patch-level feature presentation을 구성할 때local neighbourhood aggregation을 사용한다. 따라서 아래와 같이 근접한 feature vector를 통합한다. $\phi_{i,j}(h,w)$는 아래로 바뀌게 된다. 

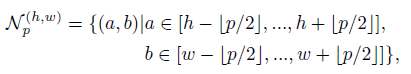
Locally aware features at position (h,w)는 아래와 같다. 

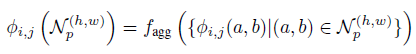
Patch core에서는 $f_{agg}$를 adaptive average pooling을 사용했다. 

그리고 Locally aware patch-feature collection은 아래처럼 표현된다. 

또한 multiple feature hierarchies 사용하는 것을 성능을 높이는 데 도움을 줄 수 있다. 하지만 feature의 generality를 유지하기 위해 j와 j+1만 사용한다. 2가지 feature를 합치기 위해서 $\mathcal{P}_{s,p}(\phi_{i, j+1})$을 bilinearly rescaling해서 $\mathcal{P}_{s,p}(\phi_{i, j})$와 매칭이 되게 하고 corresponding patch feature를 합친다. 

최종적으로 정상 훈련 셋에 대한 memory bank $M$은 아래처럼 정의된다. 

 

Coreset-reduced patch-feature memory bank

related work 링크 참조 

K-Center Greedy 알고리즘 도식화 (https://kmhana.tistory.com/6)

 

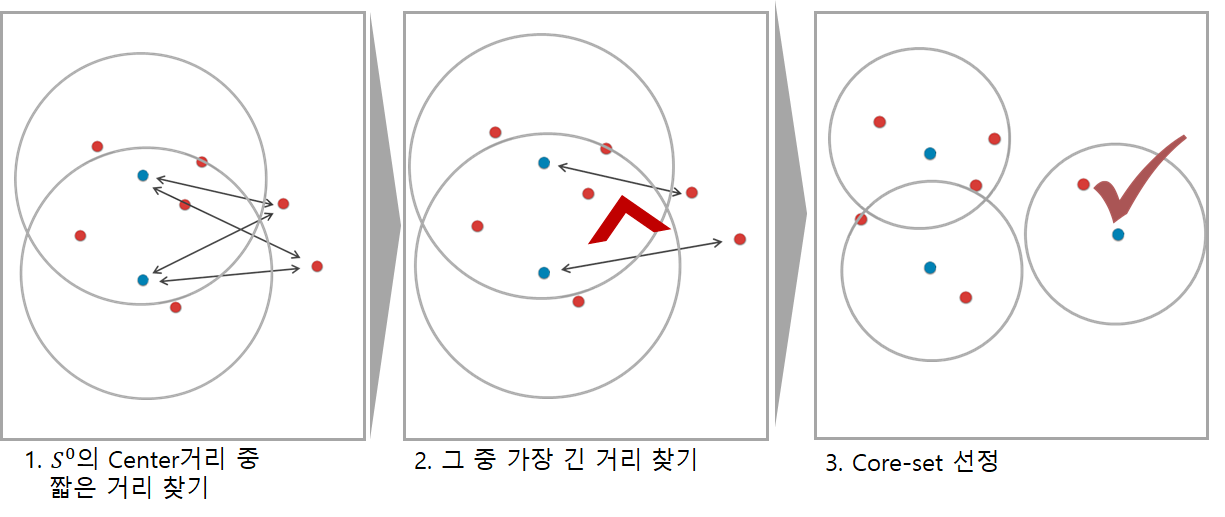
Anomaly Detection with PatchCore

한 장의 test image $x^{test}$에 대한 image anomaly score(s)를 도출하기 위해 patch collection $\mathcal{P}(x^{test}) = \mathcal{P}_{s,p}(\phi_j(x^{test}))$에 있는 test patch feature와 memory bank에 있는 each respective nearest neighbour $m^*$의 maximum distance score $s^*$를 구한다. 

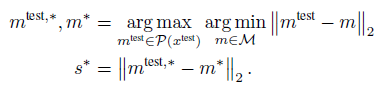
만약 memory bank가 anomaly candidate $m^{test,*}$와 가장 가까운 경우, $m^{*}$는 이웃 샘플과 멀고 흔치 않은 nominal occurence이다. 따라서 anomaly score를 증가하여 최종 스코어 s를 얻는다. 

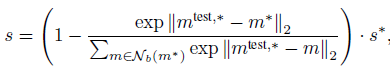
$\mathcal{N}_b(m^*)$ 는 test patch feature $m^*$ 에 대한 $M$ 안에서의 B nearest patch features이다. 이것의 의미는 현재 test image에 대해서 memory bank 안에 있는 features 중에서 가장 정상적(?)이라고 생각되는 $m^*$와 가장 가까운 patch feature를 사용한다. 정상 테스트 이미지가 들어오면 둘 간의 차이가 매우 적을 것 -> 마이너스 우항에 있는 값이 작아짐 -> 1-(*)가 작아지게 됨. (비정상 이미지인 경우에는 반대)

** 이 부분이 잘 이해가 가지 않음. 

 

s를 구하면 segmentation을 위한 step은 다음과 같이 진행된다. image-level anomaly score를 구하기 위해서 argmax 연산을 통해 each patch에 대한 anomaly score를 필요로 한다. segmentation을 위해서 patch anomaly score를 각각의 위치를 고려하여 재정렬한다. 원본 이미지 사이즈에 맞추기 위해서, bi-linear interpolation을 사용하여 upscale한다. 

 

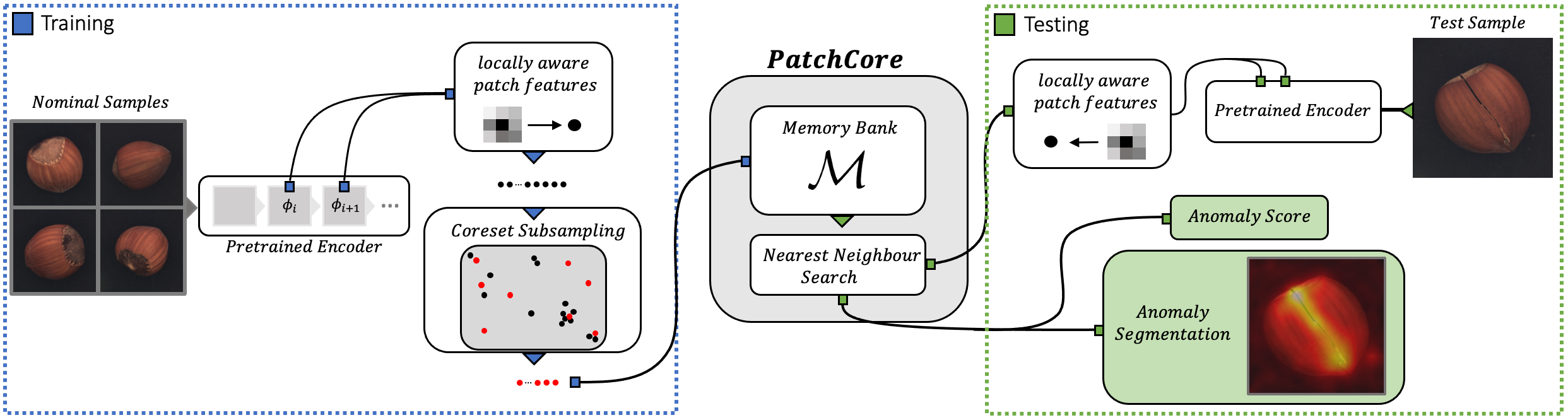
전체적인 Patch core 개념도는 다음과 같다. 

Overview of PatchCore. During training, nominal samples are broken down into a memory bank of neighbourhoodaware patch-level features. For reduced redundancy and inference time, this memory bank is downsampled via greedy coreset subsampling. At test time, images are classified as anomalies if at least on patch is anomalous, and pixel-level anomaly segmentation is generated by scoring each patch-feature.